PRD
The human brain cannot fully comprehend true random; it instead attempts to create patterns where none exist.
In megagames, an area of unprecedented societal importance, the application of random events is a crucial to generating acceptable levels of fun. When most normies envision random, they expect an equal distribution. When a random fails to represent these expectations: antifun. How can we remodel true random for intrinsic human expectations, yet still retain an acceptable representation to generate maximum fun?
Let's look at Dota 2 which, in the interests of fun, is rife with random number generator (RNG) fudge. Most of it cannot be credited to Valve, and actually has roots in the Warcraft III engine used to build the original DotA. The primary tactic being applied is psuedo-random distribution (PRD). PRDs are a statistical mechanic where an outcome's probability increases every time it fails to occur. It is an approach to normalize a statistical outcome and protect against the highly improbable's adverse impacts. PRDs are incredible equalizers when it comes to RNG. They alleviate situations where a programmed random occurrence (proc) fails to trigger over many consecutive attempts. They also normalize occurrences of the ever-present RNGesus bashlord, avatar of undeserved bullshit luck, by inhibiting consecutive triggers.
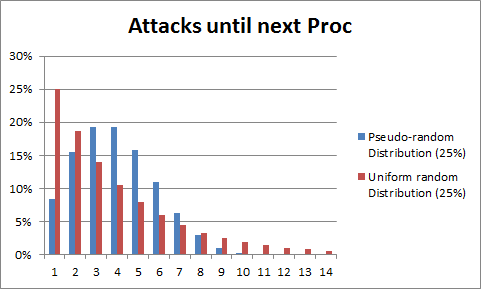
A simple example is a proc of 25% chance on attack to trigger a bash. Under standard RNG, a human would predict that on average one in every four attacks will trigger the proc. However, it is possible for two or more consecutive attacks to trigger the proc, or many consecutive attacks fail to proc. Ten consecutive misses has about a 5.6% probability, but for a human mind those ten misses with a presumed 25% proc rate can be incredibly frustrating. With a PRD implementation, one in every four attacks can still be expected by a human to be the proc average. But the probability of consecutive proc triggers is greatly reduced. Additionally, one in every twelve attacks is guaranteed to trigger the proc.
The probability of a proc on the nth attempt since the last proc is given as P(n) = C * n. C is a constant calculated from the expected probability of the modifier occurring. When P(n) becomes greater than 1.00, the proc is guaranteed. The calculation of C is complex and involved, but it vaguely represents the number of consecutive procs in a sample divided by the number of non-procs in the same sample. And because Dota 2 is pulling Warcraft III C-values for consistency, some of them are slightly adjusted from this calculation which results in actual proc rates not matching percentage descriptors in tooltips. Here is what Dota 2 uses.
Segue outside of vidya games, PRDs are very difficult to apply in the tabletop world. Layered proc rates coupled with proc history flux is demanding to track without the aid of a computerized system. Additionally, the probability calculations do not translate well to a standard dice set. Some electronic tabletop assistance programs, such as Roll20 have community pressure to adopt PRD models, but are in constant debate over their application.
Regardless, the future of random number generation within megagames is highly likely to be found with pseudo-random distributions. The ability to match psychological models results in a much more enjoyable experience.